Telescope Basics
Introduction
Astronomical telescopes are primarily used to look at celestial objects that would otherwise be too faint to observe with the naked eye. It all has to do with the fact that the pupils in our eyes can only dilate (increase in diameter) to about 7mm. The faint light that comes from distant objects has the property of travelling in (almost) parallel rays. Only a small bundle of those rays, with a diameter of about 7mm, will fit into our eye (see diagram below).
By using a lens, you can catch a much bigger bundle of the light and compress it. By using a second lens (or a set of lenses called an eyepiece), you can then reconstruct the light into a bundle with a diameter of 7mm or less, so that it fits through your pupil. During this process, only a little bit of light is lost in the optics, so the image you can see will be much brighter (see diagram below).

Aperture and Light Grasp
It should not therefore come as a surprise that the most important feature of a telescope is the size of its so-called objective lens, rather than what most people initially think, its magnification power. The diameter of the objective lens is called the aperture. The larger the aperture of the telescope, the bigger its light grasp or, in other words, the fainter the objects you can see with it.
To get an idea of how much light grasp a particular telescope has, you can divide the square of the aperture (in mm) by 49. So, for example, a telescope with an aperture of 70mm has a light grasp of 100x the human eye (79x79/49), and a telescope with an aperture of 150mm has a light grasp of 459x the human eye (150x150/49).
"The most important spec of a telescope is its aperture. The bigger, the better."
Magnification
If a telescope has an aperture of 70mm, you need to compress the bundle of light at least 10 times to make it fit through your pupil. Compressing the bundle of light has an important side effect - it makes the picture appear larger. If you compress the bundle of light 10 times, the image appears 10 times bigger. This phenomenon is referred to as the magnification of a telescope.
Some objects in the night sky are not only very dim because they are far away, they appear very small too. So, by compressing the bundle of light even more, you can effectively increase the size of the image to make it easier to see. By doing this, however, you increase the effects of minor anomalies in the optics of the telescope and those in your eyes. This means that, depending on the quality of the optics of the telescope, you would not normally want to compress the bundle of light to less than 0.5mm. In our example of a telescope with a 70mm lens, this would occur when you compress the bundle 140 times, or in other words, at a magnification of 140.
"The maximum theoretical magnification of a telescope lies usually around twice the aperture in mm."
Focus
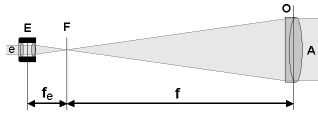
When a lens compresses a bundle of light, at some point behind the lens the bundle will be squeezed into nothing more than a point. This is called the focal point (point F in the diagram below). Beyond that point, the bundle starts to expand again. The distance from the centre of the objective lens (O) to its focal point is called the focal length (f in the diagram) and differs from lens to lens, depending on its curvature.
The relationship between aperture and focal length is another important characteristic called the focal ratio, or speed. This focal ratio is indicated by the symbol f/. So, a lens with an aperture of 70mm and a focal length of 350mm has a focal ratio of f/5. Telescopes with a short focal ratio (f/5 or less) are called fast. The terms "fast" and "speed" are derived from photography where using lenses with a short focal ratio permits the use of faster shutter speeds.
"Telescopes with fast focal ratios are most suitable for astro-photography."
The Eyepiece
Although eyepieces usually consist of more than one lens, they can be regarded optically as a single lens. In many books on telescopes, you will read that the eyepiece "magnifies the image which has been focussed by the objective lens". This description, although theoretically correct, is a bit vague. It would be much better to say that the purpose of the eyepiece is to put the expanding light rays beyond the focal point back into a bundle of parallel rays again, in order to reconstruct the image. For that purpose, the eyepiece needs to be placed exactly at the right distance from the focal point. Looking at the diagram below, you would expect this distance to be the same as the focal length(fe) of the eyepiece (E) itself, which is indeed the case.

If the eyepiece of a telescope is in the right spot, the image is 'in focus', and will appear sharp. To put the eyepiece in that spot, the telescope has a mechanical device called the focusser, which allows you to shift the eyepiece back and forth very precisely, by means of either a couple of focussing knobs, or simply by turning the eyepiece.
It should also be clear from the diagram that the longer the focal length of the eyepiece, the further the light rays have had the chance to expand before they are put back into a parallel bundle again. In other words, the larger the focal length of the eyepiece, the larger the diameter of the exiting bundle, or exit pupil (e).
Looking once more at the diagram, you can quite easily figure out that, aperture (A) divided by focal length (f) should equal exit pupil (e), divided by the focal length of the eyepiece (fe). We saw earlier that the aperture (A), divided by the exit pupil (e), represents the magnification of the telescope. So we can now conclude that you can calculate the magnification of the telescope simply by dividing the focal length of the objective lens (f) by the focal length of the eyepiece (fe). So in our example, a 70mm f/5 telescope (f = 350mm) with a 35mm eyepiece will give a magnification of 10x (350/35=10) and an exit pupil of 7mm.
"The magnification of a telescope depends on the eyepiece used."
Field of View
The amount of sky that you can view through a telescope is called the real (true) field of view and is measured in degrees of arc (angular field). The larger the field of view, the larger the area of the sky you can see. Angular field of view is calculated by dividing the power being used into the apparent field of view of the eyepiece being used. In our example (70mm f/5 telescope), if you were using a 7mm eyepiece with a 50 degree apparent field, the power of the telescope with this eyepiece would be 350/7=50x, then the field of view would be 1 degree (50/50 = 1).
Manufacturers will normally specify the apparent field (in degrees) of their eyepiece designs. The larger the apparent field of the eyepiece (in general), the larger the real field of view and thus the more sky you can see. Likewise, lower magnification allows much wider fields of view than higher magnification.
"At low magnifications you get a much bigger true field of view."
Resolution and Resolving Power
Resolution is the ability of a telescope to render detail. The higher the resolution, the finer the detail is. The larger the aperture of a telescope, the higher the resolution of the instrument will be, assuming the telescope's optics are of high quality.
The resolving power is sometimes referred to as the 'Dawes limit.' It is the ability to separate two closely spaced binary (double) stars into two distinct images measured in seconds of arc and is very closely related to the resolution. Theoretically, to determine the resolving power of a telescope, divide the aperture of the telescope (in mm) into 116. For example, the resolving power of a 70mm aperture telescope is 1.7 seconds of arc (116 divided by 70 = 1.7). Once again, the bigger the aperture, the better the resolving power. However, resolving power is often compromised by atmospheric conditions and the visual acuity of the observer.
"Resolving power is often compromised by atmospheric conditions and the visual acuity of the observer"
Limiting Magnitude
Astronomers use a system of magnitudes to indicate how bright a stellar object is. An object is said to have a certain numerical magnitude. The larger the magnitude number, the fainter the object is. Each object with an increased number (next larger magnitude number) is approximately 2.5 times fainter. The faintest star you can see with your unaided eye, with no telescope and dark skies, is about sixth magnitude, whereas the brightest stars are magnitude zero, or even a negative number.
The faintest star you can see with a telescope (under excellent seeing conditions) is referred to as the limiting magnitude. A rough formula for calculating visual limiting magnitude is: 7.5+5xLOG (aperture in cm). For example, the limiting magnitude of a 70mm aperture telescope is 11.7. (7.5+5LOG7=11.7). Atmospheric conditions and the visual acuity of the observer will often reduce limiting magnitude.
Photographic limiting magnitude is approximately two or more magnitudes fainter than visual limiting magnitude.
"On a very dark night, with the naked eye you may see stars as faint as magnitude 5 or possibly 6."
Aberrations
Aberrations are optical 'errors' which occur in most optical equipment and are usually due to lack of quality but, in most cases, they are just due to the configuration of the telescope and are either something you have to learn to live with or something that can be corrected by using additional optics or an alternative configuration.
Chromatic Aberration is the failure of a lens to bring light of different wavelengths (colours) to a common focus. This is due to the fact that light of a different wavelength (= colour) refracts (bends) at a different rate when it hits the optical glass.
This results mainly in a faint coloured halo (usually violet) around bright stars, the planets and the Moon. It also reduces lunar and planetary contrast. It usually shows up more as speed and aperture increase. By cementing two lenses together, a so-called achromatic doublet is created which can help reduce this aberration. More expensive, sophisticated telescope designs like apochromatics and those using fluorite lenses can virtually eliminate it.
Spherical Aberration is caused by light rays passing through a lens at different distances from the optical centre to come to focus at different points on the axis. This causes a star to be seen as a blurred disk rather than a sharp point. Most telescopes are designed to eliminate this aberration.
Astigmatism is a lens aberration that elongates images that change from a horizontal to a vertical position on opposite sides of best focus. It is generally associated with poorly made optics or when the optics in a telescope are not perfectly aligned.
Field curvature is caused by the fact that at the so-called focal plane (= the imaginary area where all focal points of a lens form a disk) is not flat but slightly curved. The faster the focal ratio of the lens, the more curved this focal plane becomes. The focal plane of the eyepiece is also curved, but the other way around (and more prominent in eyepieces with short focal lengths). One can expect that only where the two focal planes intercept will the image be sharp. This is why field curvature is less prominent in telescopes with longer focal ratios and at lower magnification (while using eyepieces with longer focal lengths).
"Any good telescope has so called diffraction limited optics."